7.3 Berechnen von Extrempunkten
7.3.1 Was ist ein Extrempunkt
7.3.2 Notwendige Bedingung für Extremstellen
7.3.3 Hinreichende Bedingung für Extremstellen
7.3.4 Berechnen der y-Koordinaten für Extremstellen
7.3.5 Aufgaben
7.3.1 Was ist ein Extrempunkt?
Extrempunkte sind "Berggipfel" und "Talsohlen" eines Funktionsgraphen, die Berggipfel heißen Hochpunkte oder Maxima (Einzahl Maximum), die Talsohlen heißen Tiefpunkte oder Minima (Einzahl Minimum).
Mit Extrempunkten sind hier immer lokale Extrempunkte gemeint. Das heißt es ist nicht der Punkt gemeint, an dem die Funktion insgesamt den höchsten Funktionswert hat. Wenn man den insgesamt höchsten oder tiefsten Punkt eines Funktionsgraphen meint, dann spricht man von globalen Extrempunkten.
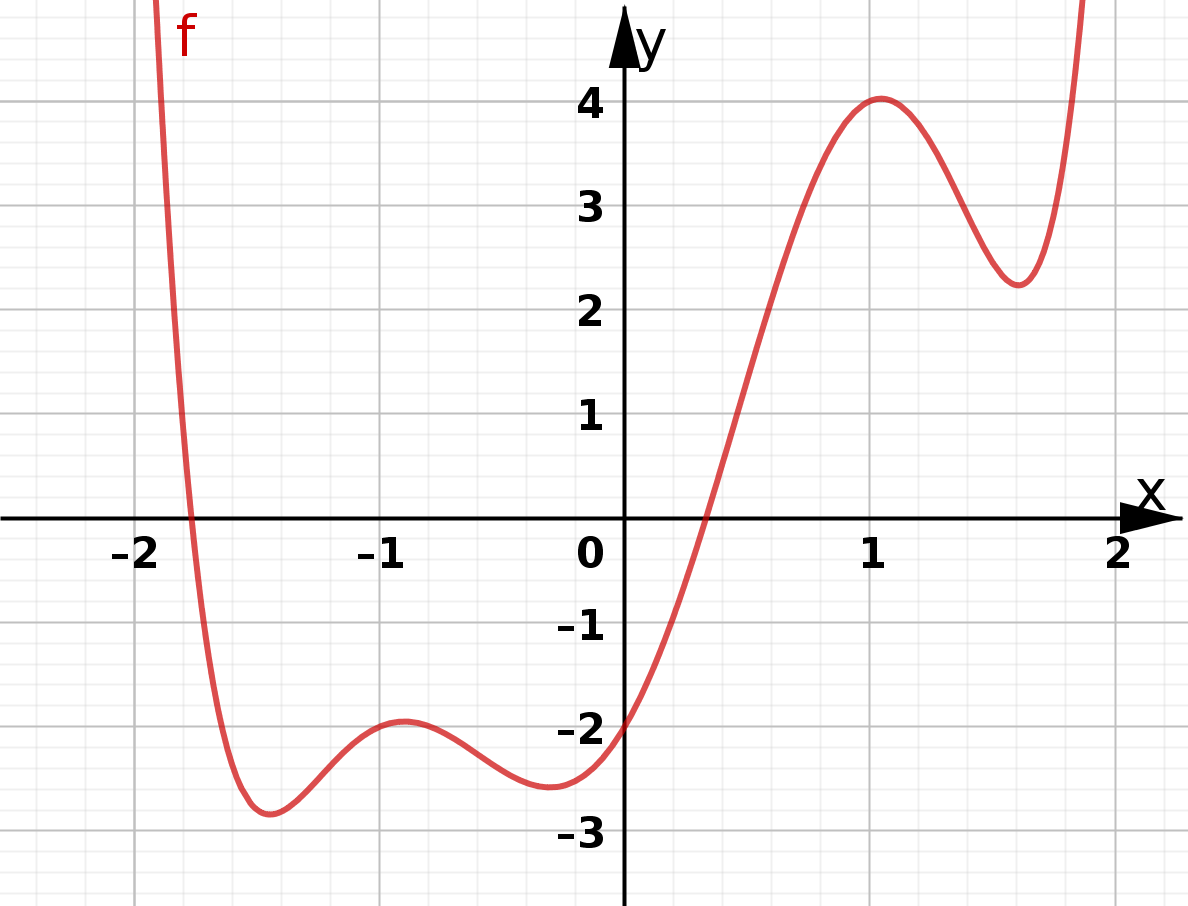
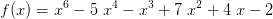
Im Beispiel oben gibt es zwei Hochpunkte und drei Tiefpunkte. Alle lokalen Extrempunkte haben gemeinsam, dass die Steigung des Funktionsgraphen in diesen Punkten gleich Null ist. Das heißt, wenn man hier eine Tangente einzeichnet, dann ist diese waagerecht:
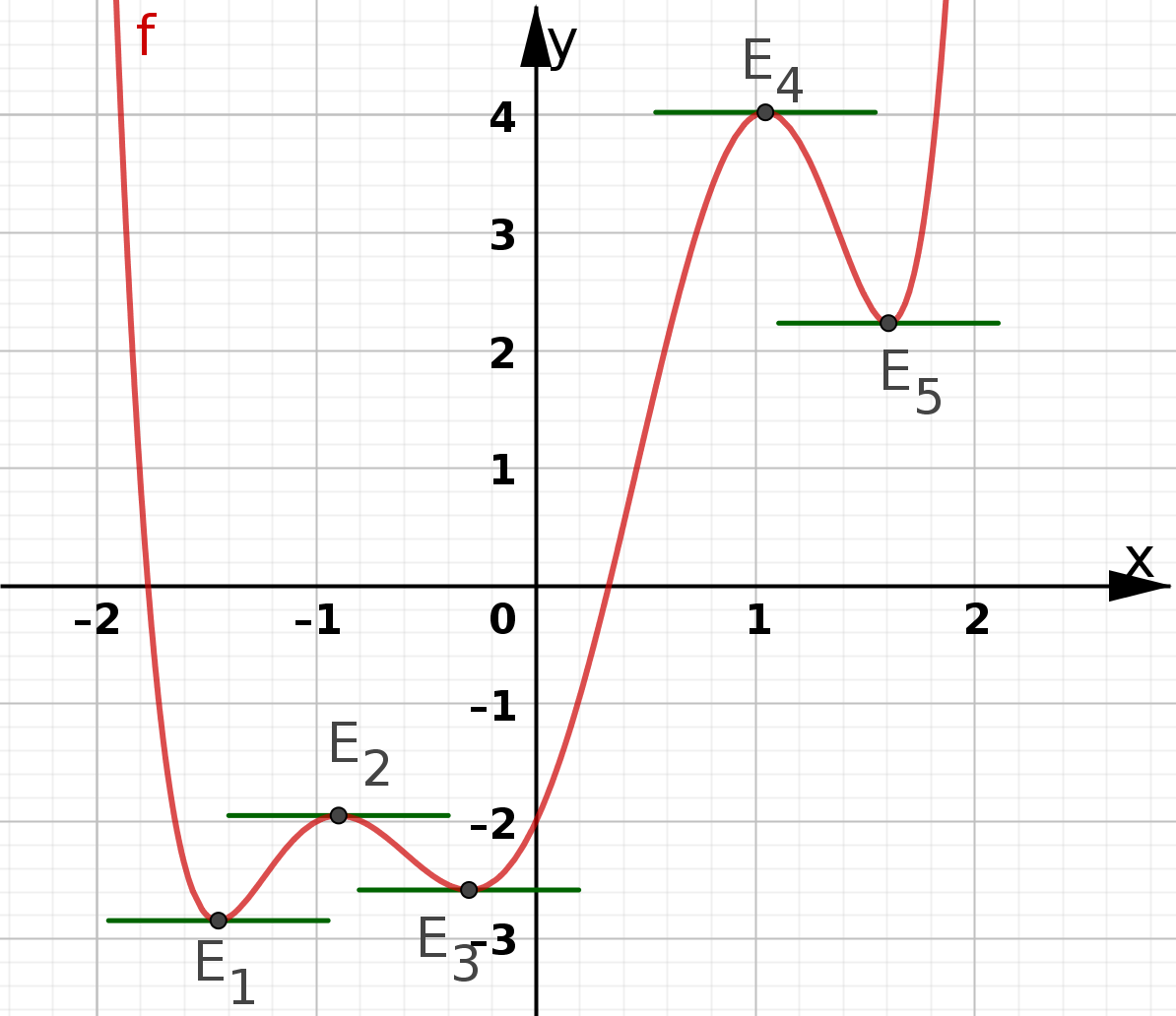
Nur wenn eine Tangente in einem Punkt waagerecht ist, kann dieser Punkt ein Hoch- oder ein Tiefpunkt sein. Daher gibt es die
7.3.2 Notwendige Bedingung für Extremstellen
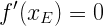
Nur wenn an einer Stelle xE der Funktionswert der ersten Ableitungsfunktion gleich null ist, nur dann ist hier eine waagerechte Tangente und nur dann kann hier ein Extrempunkt sein. Denn der Funktionswert der ersten Ableitungsfunktion gibt ja an jeder Stelle x die Steigung des Funktionsgrafen von f(x) wieder.
Aber:
Leider ist diese Bedingung noch nicht hinreichend, denn es gibt auch Funtionsgraphen wie diesen:
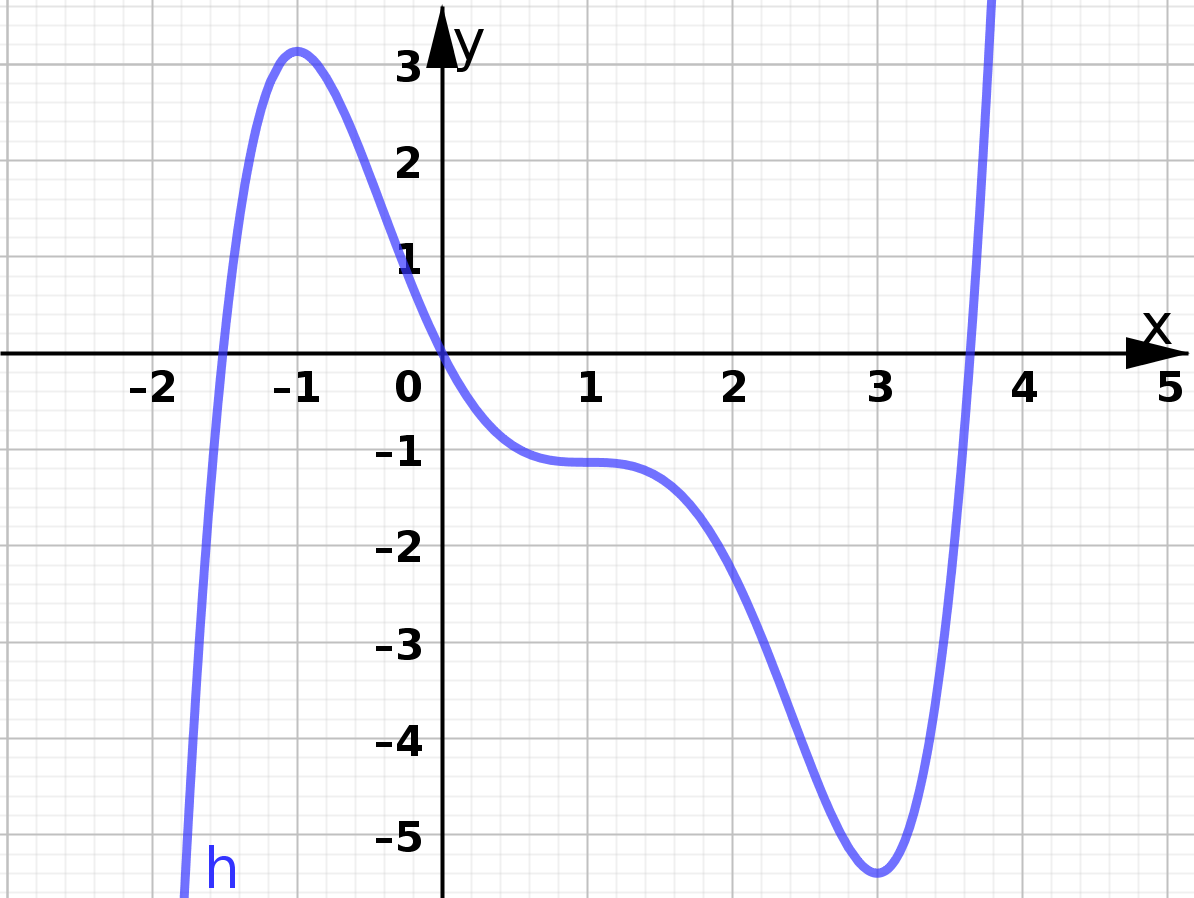
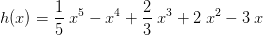
Warum +SATTELpunkt?
Hier gibt es einen Hochpunkt bei xE1 = -1, einen Tiefpunkt bei xE2=3 und einen Sattelpunkt bei xS=1
Sattelpunkte sind Punkte, in denen die erste Ableitung der Funktion gleich Null ist, bei denen aber kein Extrempunkt vorliegt.
Das Problem ist, dass Sattelpunkte auch die notwendige Bedingung für Extrempunkte erfüllen. Daher ist diese Bedingung noch nicht hinreichend (oder ausreichend)
7.3.3 Hinreichende Bedingung für Extremstellen
Wenn die notwendige Bedingung für Extrempunkte erfüllt ist, muss also noch überprüft werden, ob an dieser Stelle nicht vielleicht ein Sattelpunkt ist.
xE sei jetzt im Weiteren eine Stelle an der die Ableitung einer Funktion f gleich Null ist, es gilt also f'(xE)=0.
7.3.3.1 Die hinreichende Bedingung mit der zweiten Ableitungsfunktion
Dieses Kriterium ist am einfachsten anzuwenden und daher in den meisten Fällen empfohlen. Es verwendet den Krümmungssinn des Funktionsgraphen (siehe 7.2):
f''(xE)>0 : Wenn an einer Stelle xE die zweite Ableitungsfunktion einen positiven Funktionswert hat, dann liegt hier eine Linkskrümmung vor und dann muss hier ein Tiefpunkt sein.
f''(xE)<0 : Wenn an einer Stelle xE die zweite Ableitungsfunktion einen negativen Funktionswert hat, dann liegt hier eine Rechtskrümmung vor und dann muss hier ein Hochpunkt sein.
f''(xE)=0 : Wenn an einer Stelle xE die zweite Ableitungsfunktion gleich Null ist, und wenn hier die hinreichende Bedingung für einen Wendepunkt (siehe 7.4) erfüllt ist, dann ist hier ein Sattelpunkt.
Zusammengefasst:
Bei xE=0 könnte also auch ein Sattelpunkt sein. Hier kann z.B. das nächste Kriterium zur Klärung herangezogen werden:
7.3.3.2 Hinreichende Bedingung mit dem Vorzeichenwechselkriterium für die erste Ableitungsfunktion
- Wenn die Steigung vor der Stelle xE negativ und hinter der Stelle xE positiv ist, dann muss bei xE ein Tiefpunkt liegen. Hier hat sich an der Stelle xE also das Vorzeichen der Funktionswerte der ersten Ableitungsfunktion geändert.
- Wenn die Steigung vor der Stelle xE positiv und hinter der Stelle xE negativ ist, dann muss bei xE ein Hochpunkt liegen. Hier hat sich an der Stelle xE also auch das Vorzeichen der Funktionswerte der ersten Ableitungsfunktion geändert.
- In allen anderen Fällen, wenn die Steigung vor und hinter der Stelle xE positiv oder vor und hinter der Stelle xE negativ ist, dann liegt bei xE ein Sattelpunkt vor.
Das heißt auch, wenn die Ableitungsfunktion eine doppelte, eine vierfache oder eine anderes geradzahliges Vielfaches in einer Nullstelle hat, dann wird der Funktionsgraph hier nur berührt und es liegt ein Sattelpunkt vor (siehe mehrfache Nullstellen).
7.3.4 Berechnen der y-Koordinaten der Extrempunkte
Mit der notwendigen und der hinreichenden Bedingung rechnet man nur die Extremstellen aus, also die x-Koordinaten der Extrempunkte. Um die Extrempunkte zu berechnen, müssen nun noch die Extremstellen in die Funktionsgleichung f(x) eingesetzt werden.
Die Extrempunkte mit x- und y-Koordinate lauten dann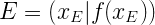 
Beispiel
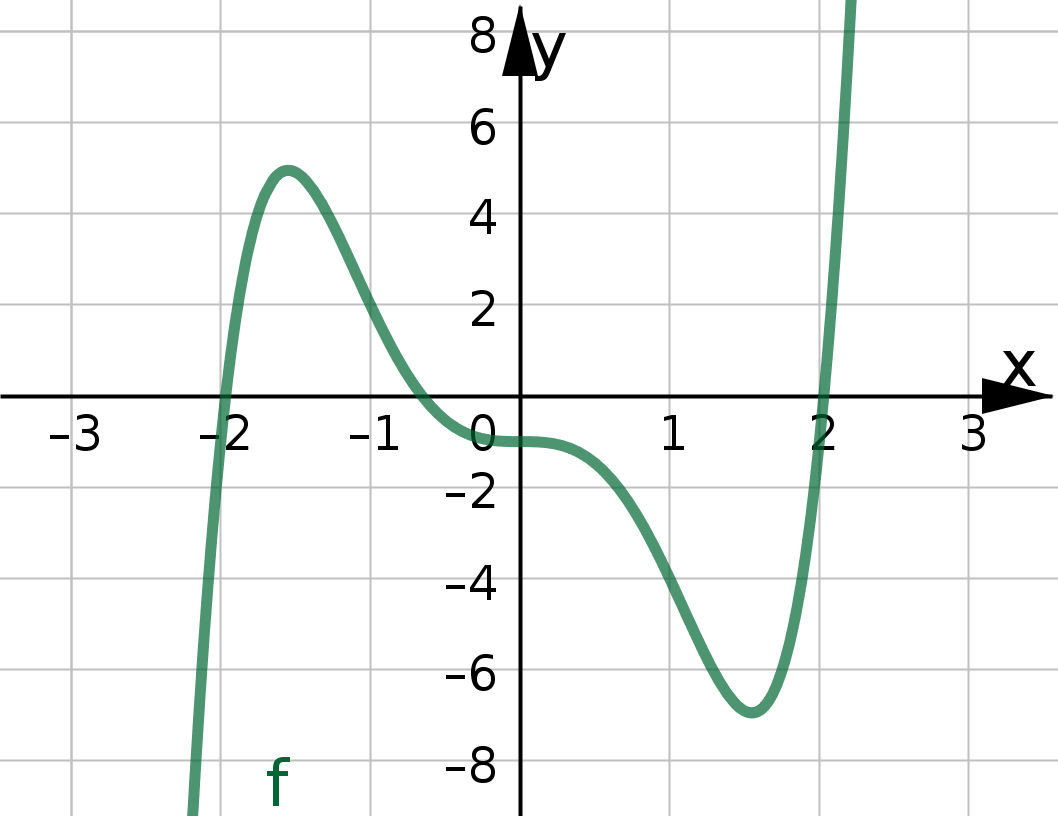
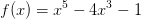
Die ersten beiden Ableitungsfunktionen von f(x) lauten:
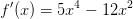und 
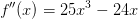
Notwendige Bedingung für Extrema :
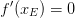
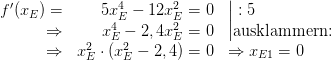
Hier liegt eine doppelte Nullstelle bei xE=0 vor, also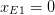 
.
Für die restlichen Nullstellen der ersten Ableitungsfunktion muss die Klammer gleich Null gesetzt werden: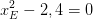 
daraus folgt 
und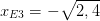 
Hinreichende Bedingung für Extrema: Einsetzen der berechneten Extremstellen in die zweite Ableitungsfunktion
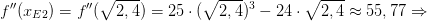Hier liegt ein Tiefpunkt vor
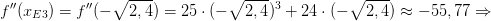Hier liegt ein Hochpunkt vor
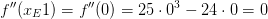Hier ist die hinreichende Bedingung nicht erfüllt und es muss weitere Untersuchungen geben
Eine Möglichkeit ist, die Stelle darauf zu untersuchen, ob es eine Wendestelle ist (siehe → 7.4 ). Sattelpunkte sind nichts anderes als Wendestellen, bei denen die Steigung gleich Null ist.
Für die hinreicheichende Bedingung für Wendestellen setzt man die Stelle xE=0 in die dritte Ableitung ein: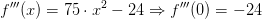 
In Kapitel 7.4 werden wir lernen, dass hier offenbar ein Wendepunkt mit einer maximalen Steigung vorliegt . Das mag auf den ersten Blick auf den Funktionsgraphen etwas verwirren, denn die Steigungen rund um x=0 sind alle negativ. Aber genau deshalb ist hier x=0 ein Maximum in der Steigung.
Heranziehen des Vorzeichenwechslkriteriums:
Da sich in der ersten Ableitung ein x2 ausklammern lässt, liegt hier eine doppelte Nullstelle in der ersten Ableitung vor (siehe → mehrfache Nullstellen). Der Funktionsgraph der ersten Ableitung berührt hier also nur die Abszisse. Damit geschieht hier kein Vorzeichenwechsel und somit ist hier ein Sattelpunkt.
Berechnen der y-Koordinaten
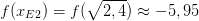, das heißt die Koordinaten des Tiefpunktes sind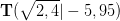 
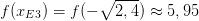, das heißt die Koordinaten des Hochpunktes sind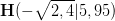 
7.3.5 Aufgaben
Aufgaben mit Anwendungsbezug: (pdf)