8.3 Integralrechnung nach Riemann - die Bedeutung des Differentials

Ein Beispiel für die Berechnung einer Fläche unter einem Grafen im Intervall [0 ; x_max] mit Riemannscher Streifenzerlegung

Das Berechnen von Flächen mit den Regeln der Geometrie gelingt normalerweise nur mit bekannten einfachen geometrischen Objekten, wie Vielecke, Kreise oder Ellipsen. Dafür gibt es jeweils eine Lösungsformel, die sich in jeder Formelsammlung nachschlagen lässt.
Die Integration ermöglicht die Berechnung einer Fläche zwischen einem beliebigen Funktionsgrafen f(x) und der Abszisse. Die Herleitung so einer Flächenberechnung stammt von Georg Friedrich Bernhard Riemann (1826-1866). Die Idee soll hier beispielhaft an der Funktion f(x)=x² gezeigt werden.

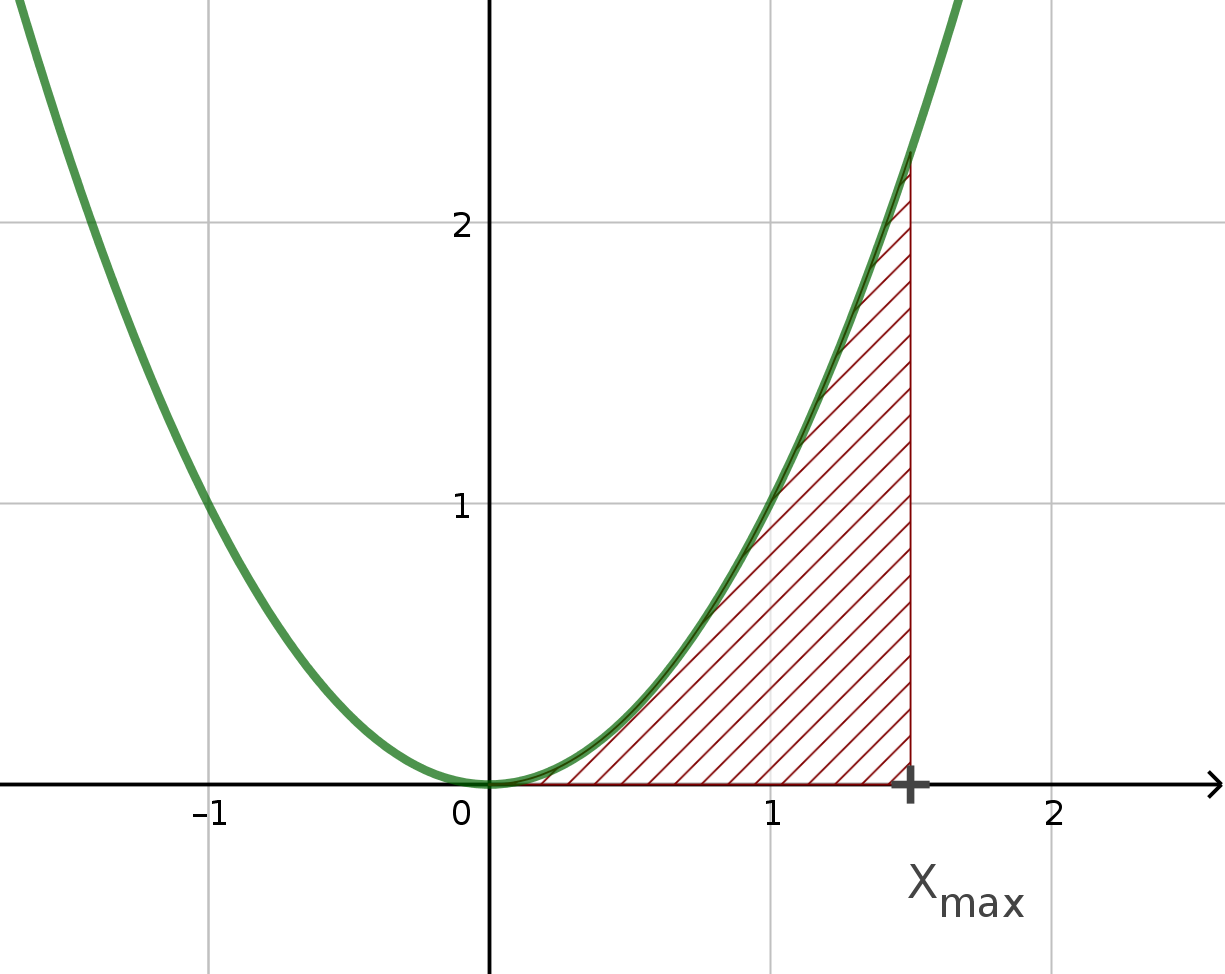
Riemann kam auf die Idee, die Fläche als eine erste Näherung zuerst in lauter senkrechte Streifen zu unterteilen. In der Abbildung ist die Fläche in 10 Streifen unterteilt worden. Die Höhe der Streifen ist jeweils der Funktionswert an der rechten Streifenseite und die Breite eines Streifens ist .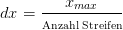

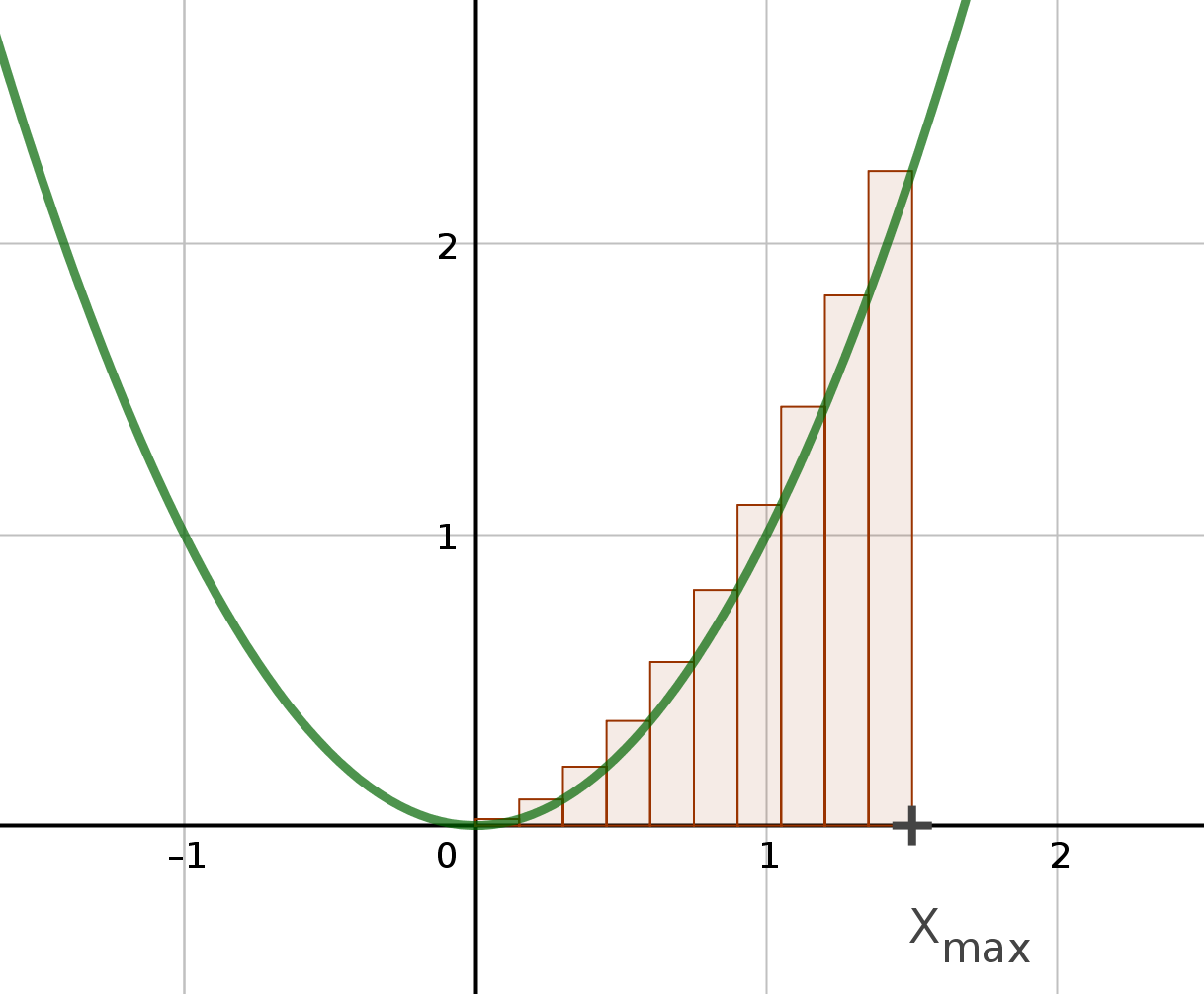
Natürlich ist dies nur eine Näherung für die tatsächliche Fläche unter dem Funktionsgrafen. Aber die Rechnung kann beliebig genau gemacht werden, in dem man einfach die Anzahl der Streifen erhöht. Die einzelnen Streifen selbst werden dann immer schmaler.
Mathematisch kann man die Fläche sogar in unendlich viele und damit auch unendlich schmale Streifen unterteilen, und dann ist das Ergebnis die exakte Fläche unter dem Funktionsgrafen.

Wer diese Rechnung ansehen möchte, wie man mit unendlich vielen Streifen rechnet, der mag unter diesem Link nachschauen: Riemann'sche Streifenzerlegung

Zur Schreibweise von Integralen

Riemann hat die Flächen unter einem Funktionsgraphen in Balken aufgeteilt. Jeder Balken hat die Höhe f(x) und die Breite dx. Das heißt die Fläche eines Balkens ist f(x) · dx.
Das Integral ist die Summe der unendlich vielen Flächen f(x) · dx. Deshalb schreibt man vor diese Flächen ein ∫ . also F(x)=∫ f(x) · dx

Integrale und negative Flächen

Wenn man sich die Herleitung der Integralrechnung nach Riemann ansieht, dann wird unmittelbar klar, dass Integrale etwas mit Flächen zu tun haben.
Der Funktionswert einer Stammfunktion gibt offenbar die Fläche zwischen dem Funktionsgraphen und der Abszisse wieder, mit dieser Idee hat Riemann die Integralrechnung entwickelt.

Nicht Fläche, sondern Flächenbilanz

Das knappe Beispiel oben unterschlägt aber eine wichtige Folge der Riemannschen Idee. Dazu kann man sich die folgende Funktion ansehen:

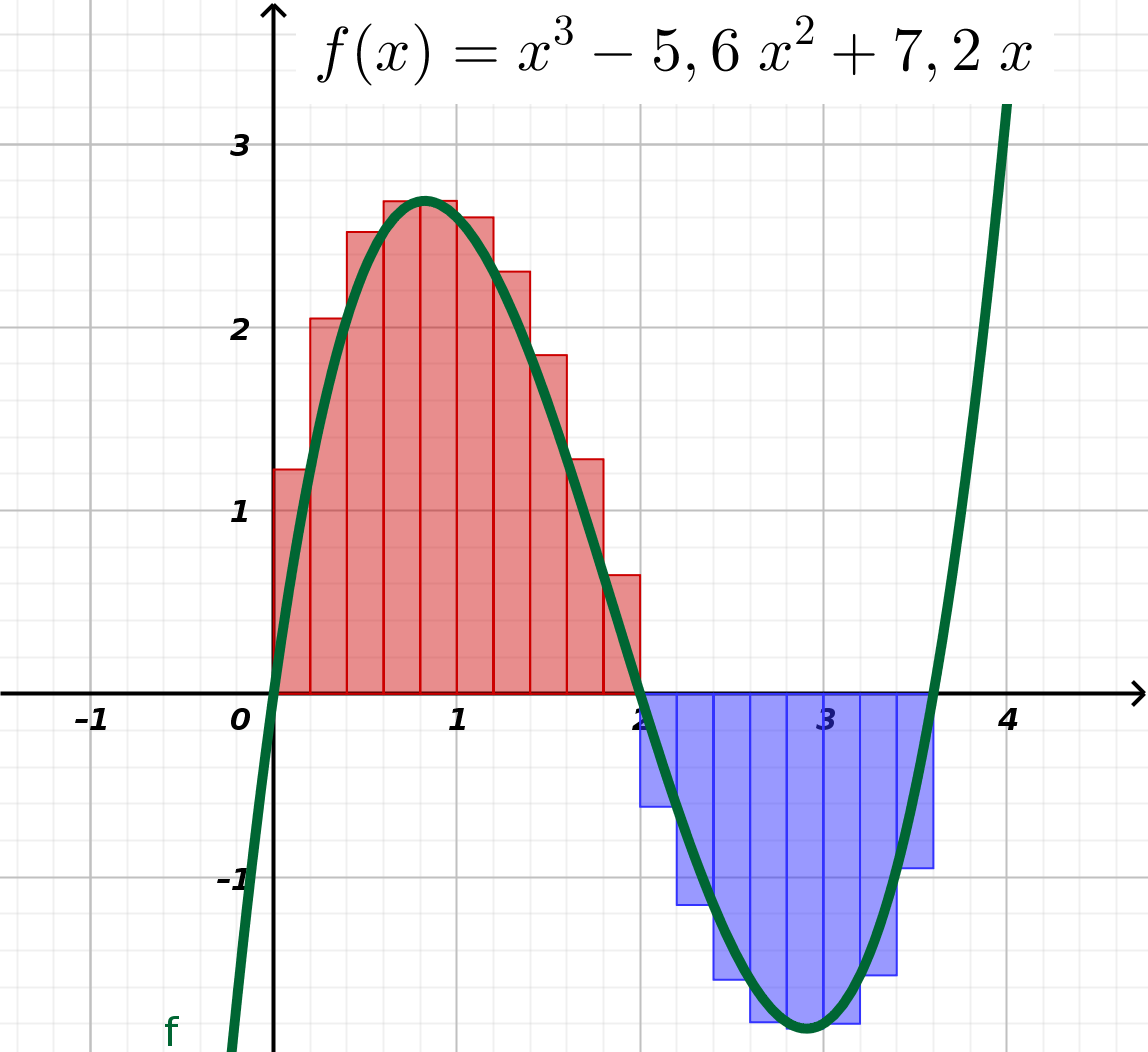
Die Fläche unter dem Funktionsgraphen von f(x) hat Riemann durch Ober- und Untersummen angenähert. Das heißt er hat die Fläche in Rechtecke - senkrechte Streifen - zerlegt und deren Flächen dann addiert. Die Fläche eines Streifens ist schnell berechnet, das ist der Funktionswert f(x) an dieser Stelle multipliziert mit der Streifenbreite dx.
Was aber, wenn der Funktionswert negativ ist, wie oben im Intervall [ 2 ; 3,6 ]? Dann berechnet man nach diesem Rezept hier eine negative Fläche. Das Integral über eine Funktion f(x) in einem Intervall [a ; b] ist daher auch nicht die Fläche zwischen dem Graphen der Funktion f(x) und der Abszisse, sondern die Flächenbilanz. Das heißt hier werden positive Flächen und negative Flächen addiert. Ist die Zahl, die dabei herauskommt positiv, dann war der Anteil der positiven Fläche größer als der der negativen:

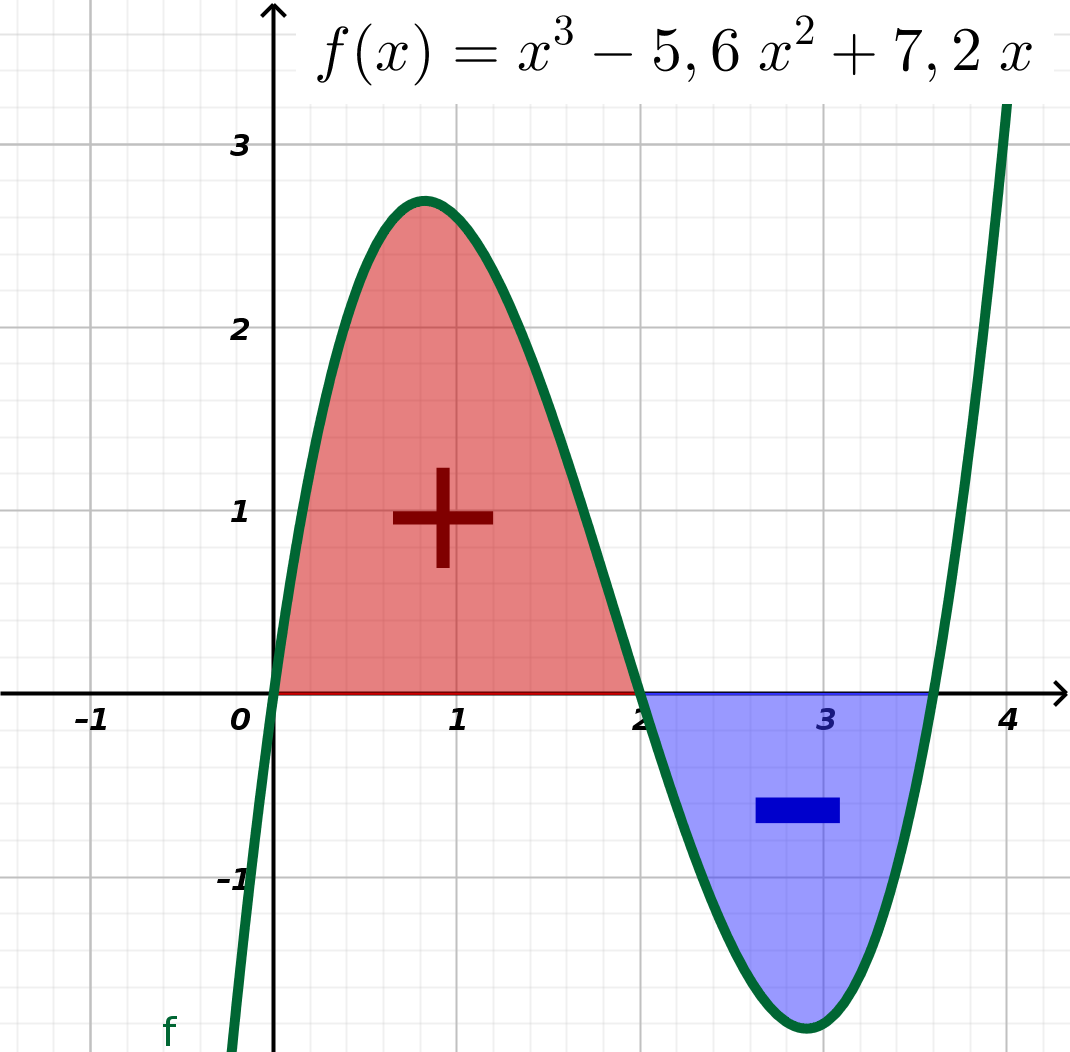
In diesem Beispiel ist offenbar der rote positive Teil größer als der blaue negative Teil der Fläche. Das lässt sich rechnerisch überprüfen:

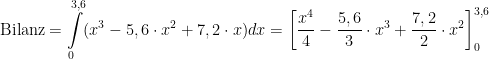
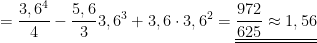
Berechnen von Flächen

Wer also wirklich eine Fläche zwischen einem Funktionsgraphen und der Abszisse bestimmen möchte, muss erst einmal positive von negativen Flächen trennen. Wenn man diese einzeln berechnet, und nur deren Beträge addiert, dann erhält man tatsächlich die Fläche:

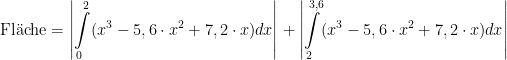
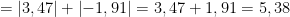
Hier wurden die Integrationsgrenzen also so gewählt, dass einmal nur über die positive und einmal nur über die negative Fläche integriert wurdse. Das geht natürlich nur, wenn man vorher die Nullstellen berechnet hat.