1.1 Schwingungen - Einführung

Eine Schwingung ist zum Beispiel die Membran eines Lautsprechers, wenn Musik gespielt wird. Diese kann an einer bestimmten Stelle des Lautsprechers zum Beispiel so aussehen:

Dies ist eine sehr komplizierte Schwingung und sehr schwer mathematisch zu beschreiben. Außerdem ist die abgebildete Schwingung nicht periodisch, denn es handelt sich nicht um ein Signal, dass immer wieder in gleicher Form wiederholt wird.

Wir betrachten im Folgenden nur periodische Schwingungen, die könnten zum Beispiel so aussehen:

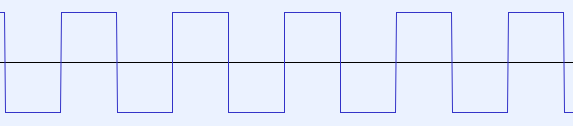
das ist eine "Rechtecks-Schwingung"

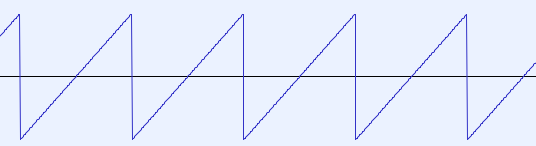
eine "Sägezahn-Schwingung"
oder

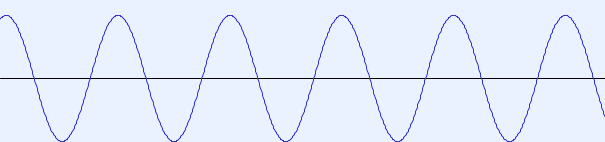
eine "Sinus-Schwingung"

In der Physik ist eine sinusförmige Schwingung eine harmonische Schwingung

Bei einer harmonischen Schwingung

... besteht die Schwingungsgleichung aus einer Sinus- oder einer Cosinus-Funktion
... ist die rückstellende Kraft proportional zur Auslenkung aus der Gleichgewichtslage

Harmonische Schwingungen sind in der Physik wichtig,

weil sie sich leicht mathematisch beschreiben lassen
weil jede periodische Schwingung sich durch eine Überlagerung von mehreren harmonischen Schwingungen erzeugen lässt.

Daher müssen wir uns im Folgenden die Sinusfunktion genauer ansehen:

1.1 Schwingungen - Einführung

Bei einer harmonischen Schwingung

1.1 Mathematische Eigenschaften der Sinusfunktion

1.2 Die Schwingungsgleichung einer harmonischen Schwingung

1.3 Die Ableitungen der Schwingungsfunktion